지난 포스팅에서는, 최소제곱법이(Method of Least Sqaure) 아닌 평균제곱오차(Mean Sqaured Error)를 활용하여 최적의 회귀선을 찾아가는 방법에 대해서 알아보았다.
2022.06.22 - [파이썬(Python), 머신러닝, 딥러닝] - 딥러닝 기초 - (3)선형회귀(평균제곱오차 / Mean Squared Error) / 파이썬 코딩
딥러닝 기초 - (3)선형회귀(평균제곱오차 / Mean Squared Error) / 파이썬 코딩
이전에 알아본 최소제곱법을 이용한 예측선을 만드는 선형회귀방법에서는, 독립변수(x)가 한 개 였기때문에 큰 문제가 없었으나, x가 여러개로 늘어나게되면 식이 점차 복잡해져 계산에 무리
goodsarah.tistory.com
즉, 최초의 임의의 회귀선 후보를 통해 실제 데이터와의 오차를 구하고, 그 오차들에 제곱을하여 평균을 낸 값이 얼마나 작은지 비교하여, 가장 작은 오차값을 만드는 회귀선을 찾아가는 방법이라고 했었는데,
그런데, 여기서 문제가 발생한다.
도대체 어느 정도만큼의 크기로 기울기와 y절편을 변화시켜야할까?
경우의 수를 따져봐도, 실수 범위내이기때문에 무한대라는 말도 안되는 경우의 수가 나오게되기에 우리는 이를 찾아가는 방법론을 생각해내야한다. 그러한 방법론 중 하나가 바로 경사하강법(Gradient descent)이다.
1. 경사하강법(Gradeint Descent) 과 학습률(Learning Rate)
선형 회귀는, 실제 y값과 예측된 y값의 차이를 최소로하는 회귀선을 찾는 것이며,
가장 효과적으로 사용할 수 있는 방법은,
손실함수(Loss Fuction)을 (y - y')의 제곱이 되며, 이를 최소로 만드는 독립변수( ex. x )를 찾아가는 방법이다.
이를 식으로 표현해보면, Loss = (y - y')^2 이다.
이때, (y-y')을 X로 치환해서 표현하면 아래의 식과 같다.

즉, 완전 제곱식의 최소값을 구하는 것이며, 완전 제곱식의 최소값은 미분값이 0 이 되는 가운데 지점인 것이다.
식을 세워서 풀면 참 쉽겠으나, 지난번에도 얘기했듯 변수와 관측값들이 많아지면 많아질수록 계산이 복잡해지고 계산 시간이 늘어나게 된다.
이를 위해 사용하는 것이 경사하강법이다.
경사하강법이란, 오차의 변화에 따라 이차 함수 그래프를 만들고, 적절한 학습률을 설정해 미분 값이 0인 지점을 구하는 것을 말한다.

위의 그림을 통해 설명해보자면,
앞서 얘기했던 것처럼, 오차를 정의하고, 그 오차의 제곱값들의 합을 구해 가장 작은 오차의 제곱값들의 합을 구하는 지점에서의 각 변수들의 계수와 y절편의 값을 구하면, 우리가 원하는 최적의 회귀식이 나오게된다.
결론적으로 위 그래프의 미분값이 0이되는 지점을 찾아가야하는데, 이때 경사하강법을 적용한다는 것은
1) 임의점을 선정하고, 해당 점에서의 미분값을 구한다.
2) 해당 지점에서 구한 기울기(미분값)의 반대 방향 (구한 값이 +면 -로, -면 +로)으로 얼마간 이동시킨 다음
3) 다시 해당지점에서 미분값을 구하고, 해당 지점의 미분값이 0이 아니라면,
4) 3)번 지점에서 구한 기울기의 반대 방향으로 얼마간 이동시키고,
................
위와 같은 작업을 반복하다가, 미분값이 0인 지점에 도달하게되면 멈추는 방법이 바로 경사하강법이다.
여기에서 "얼마간 이동시킨다" 에서 얼마만큼을 우리는 학습률(Learning rate)라고 한다. 이때 학습률을 어떻게 정의하는지에 따라서, 보다 정확하고 빠르게 미분값이 0이되는 지점을 찾아낼 수 있다.

위 그림에서 보듯 학습률이 크다면, 초기에는 빠르게 학습이 되겠지만 결국에는 큰 학습률로 인해 미분값이 0인 지점에 도달하지 못하게되는 경우가 생기게되고
학습률이 충분히 작다면, 결국에는 0인 지점에 도달하게 되겠지만, 계산에 대한 노력과 시간이 많이 들 것이다.
(학습률에 대해서는 더 다룰 내용이 많으나 우선은 이 정도로...)
그렇기에 모델별 적절한 학습률을 도입하는 것도 중요한 과정 중에 하나이다.
2. 파이썬을 통한 선형 회귀 - 경사하강법(Gradient Descent) 이용
먼저, 데이터 생성을 위한 numpy 라이브러리와 시각화를 위한 matplotlib라이브러리의 pyplot 모듈을 호출한다
# 데이터 생성을 위한 numpy 라이브러리와
# 시각화를 위한 matplotlib 라이브러리의 pyplot 모듈을 호출한다.
import numpy as np
import matplotlib.pyplot as plt
# 분석을 위한 데이터 생성
x = np.array([1, 2, 3, 4, 6, 8])
y = np.array([77,81, 85, 93, 91, 97])
#데이터의 시각화
plt.scatter(x,y, color='red', label = 'data');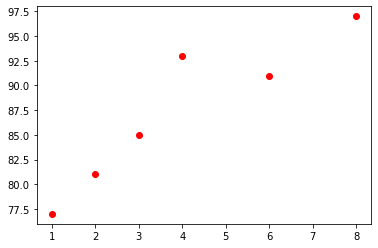
이제 경사하강법을 토해 회귀식을 구해본다
#구하고자하는 기울기(a)와 y 절편(b)을 0으로 초기화
a = 0
b = 0
#학습률(learning rate) 설정
lr = 0.03 # 일반적으로 가장 많이 쓰이는 학습률은 0.03
epochs = 1500 #반복 횟수를 설정한다. 이번 실습에서는 경사하강법을 반복하는 횟수이다.
n = len(x)
#경사하강법을 활용한 회귀식 구하기
# x 값이 총 몇 개인지 셉니다.
n=len(x)
# 경사 하강법을 시작합니다.
for i in range(epochs): # 에포크 수 만큼 반복
y_pred = a * x + b # 예측 값을 구하는 식입니다.
error = y - y_pred # 실제 값과 비교한 오차를 error로 놓습니다.
a_diff = (2/n) * sum(-x * (error)) # 오차 함수를 a로 편미분한 값입니다.
b_diff = (2/n) * sum(-(error)) # 오차 함수를 b로 편미분한 값입니다.
a = a - lr * a_diff # 학습률을 곱해 기존의 a 값을 업데이트합니다.
b = b - lr * b_diff # 학습률을 곱해 기존의 b 값을 업데이트합니다.
if i % 100 == 0: # 100번 반복될 때마다 현재의 a 값, b 값을 출력합니다.
print("epoch=%.f, 기울기=%.04f, 절편=%.04f" % (i, a, b))
결과는 위와 같이 도출된다.
결과를 해석해보면
1) 기울기와 절편이 수렴한 것으로 보아, 학습률 0.003은 목표값들이 수렴하기에 적절한 수치이다.
2) 약 400번의 반복시행부터 수렴값에 근접해갔고, 1000번의 반복시행 어간에서 기울기와 절편이 특정값에 수렴하게되었음을 확인할 수 있다.
3) 우리가 찾고자하는 최적의 회귀식의 기울기는 2.7059 이며, 절편은 76.5098이다.
즉, 우리가 찾고자하는 회귀식은 y = 2.7059 x + 76.5098 이다.
결과를 그래프로써 도출하여확인해보면
#데이터의 시각화
plt.scatter(x,y, color='red', label = 'data')
plt.plot(x,a*x + b, color='blue', label = 'linar regression line')
plt.legend()
plt.show()
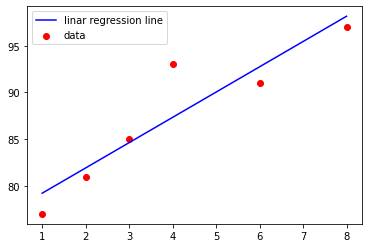
위와 같이 결과가 도출된다.
지금까지는 개념 이해와 시각화를 편하게 하기위해서, 독수가 1개인 경우로만 예시를 들어왔다.
하지만, 현실에는 특정 값에 대해 영향을 미치는 요인들(변수들)은 굉장히 많다.
그렇기에 우리는 다중선형회귀분석(변수가 여러개)에 대해서 알아보아야 한다.
변수가 많아졌다고 하더라도, 변수가 1개일때의 개념을 확장한 것이므로 동일한 논리를 적용하면되며, 점차 복잡해지는 식은 파이썬이 열심히 일하면서 결과를 도출해줄테니,
우리는 데이터프레임을 잘 작성하고, 코드만 올바르게 적용하게되면, 남아있는 일은 해석을 하는 것 뿐이다.
이 부분들은 다음 포스팅에서 알아보도록 하겠다.
'파이썬(Python), 머신러닝, 딥러닝' 카테고리의 다른 글
| 딥러닝에서 중간층을 은닉층이라 부르는 이유? (0) | 2022.08.02 |
|---|---|
| (파이썬 코드)다중퍼셉트론으로 XOR문제 해결하기 (0) | 2022.08.02 |
| 딥러닝 기초 - (3)선형회귀(평균제곱오차 / Mean Squared Error) / 파이썬 코딩 (0) | 2022.06.22 |
| 딥러닝 기초 - (2)선형회귀(최소제곱법) - 파이썬으로 코딩 (0) | 2022.06.22 |
| 딥러닝 기초 - (1) 선형 회귀(Linear regression) 개념 (0) | 2022.06.21 |




댓글